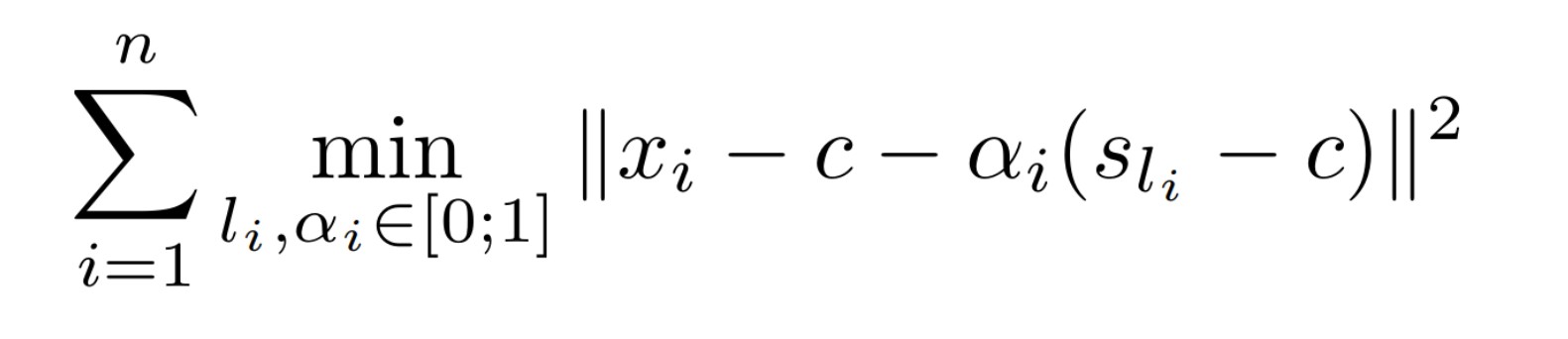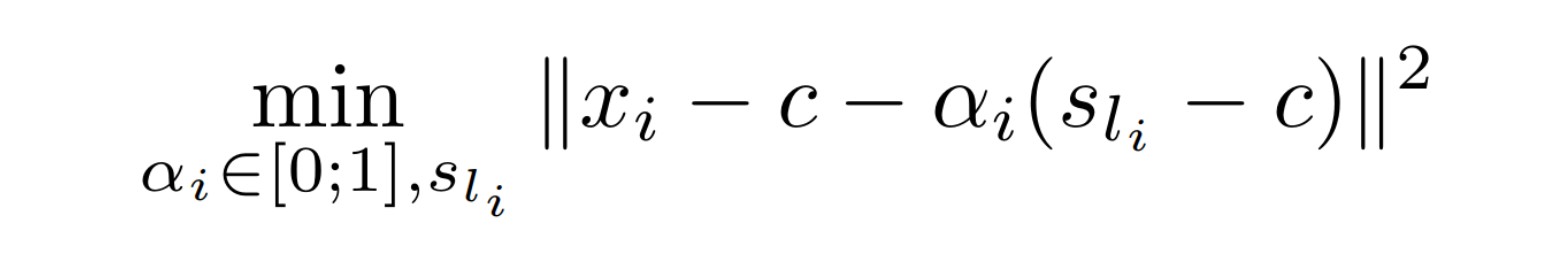项目需要,先开个坑,啥时候填完也不知道
Product Quantization
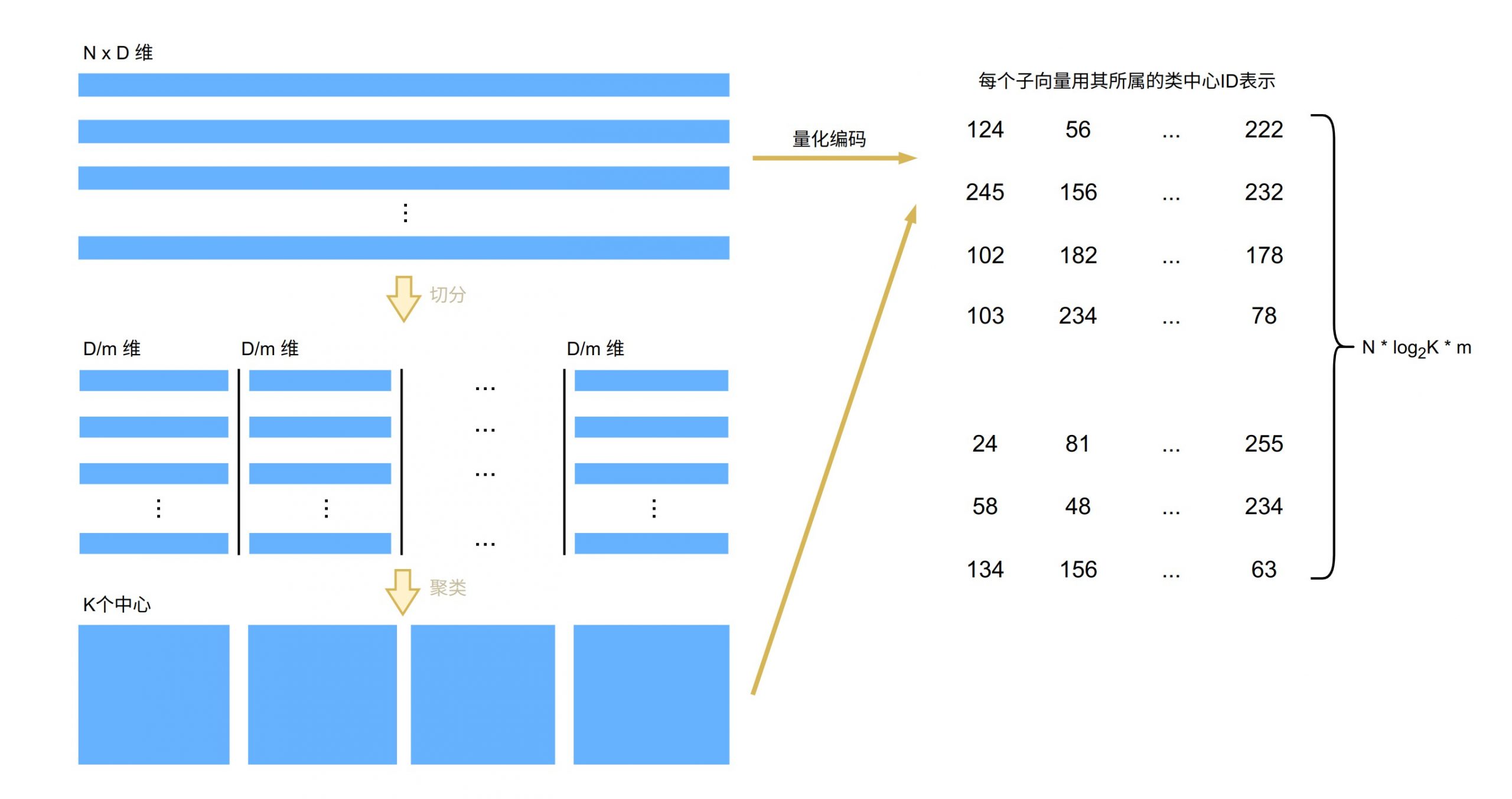
PQ(Product Quantization)是一种压缩技术,由 Herve Jegou 等学者在 PAMI2011 上发表了该算法的第一篇正式论文,用于解决相似搜索问题(Similarity Search)。其核心思想是将空间分解为若干个低维子空间的笛卡尔乘积(Cartesian product ),并对每一个子空间进行量化(Quantization),基本原理可以用下图展示。
假设原始数据集的大小为 n,向量维度为 D,数据首先会被切分为 D/m 组 m 维的子向量。对每一组子向量,可以使用 K-means 聚类得到 K 个聚类中心,这些中心点被称为码本(Codebook)。
对于每个样本向量,可以利用码本找到距离其每个子向量最近的中心点,从而使用中心点 ID 来表示子向量,完成样本的编码。假设聚类了 K 个中心点,则需要用到 n_k 位来记录中心点 ID,那么原始向量只需要使用 m * n_k 位来表示,从而大大降低了存储开销。
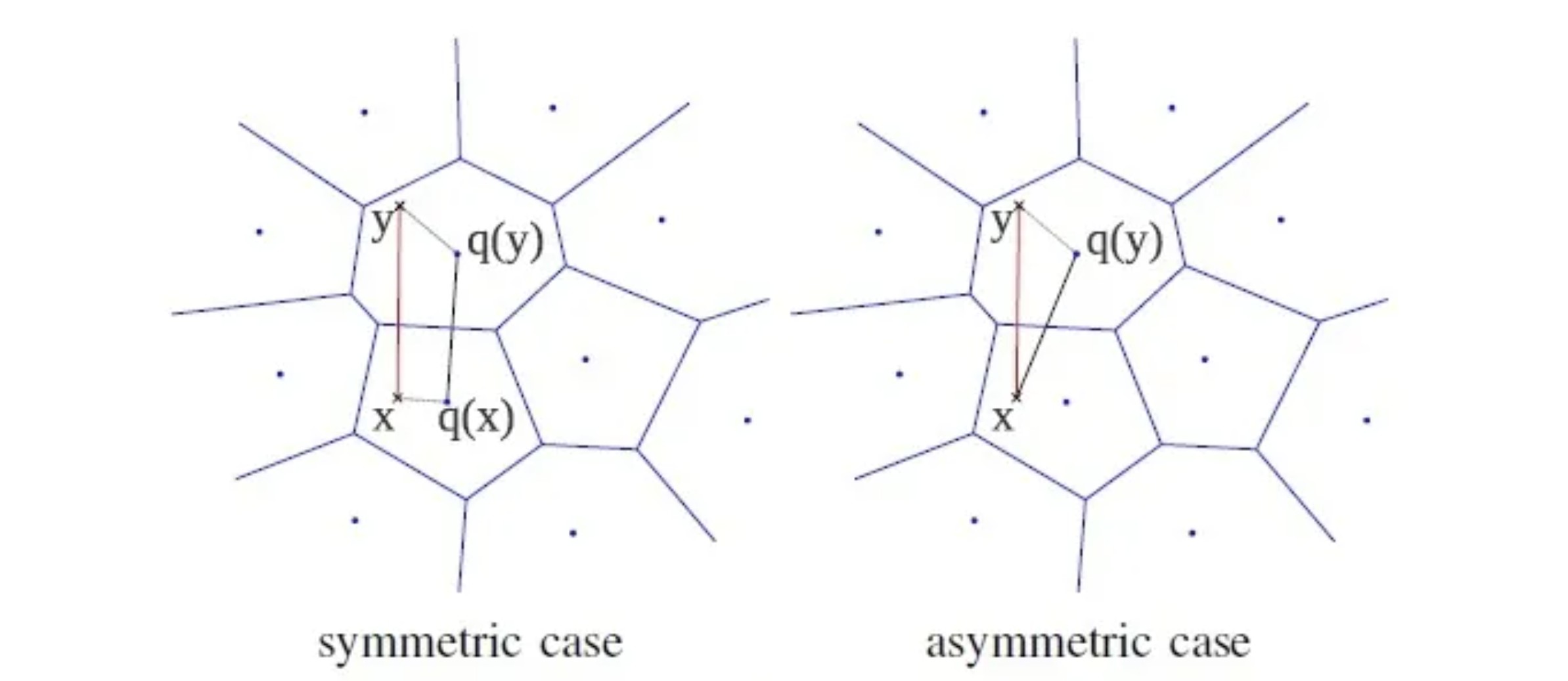
基于 PQ 的相似搜索有两种方法:一种是 SDC(Symmetric Distance Computation),即将查询向量进行量化,再与量化后的样本数据进行距离度量;另一种是 ADC(Asymmetric Distance Computation),直接使用原始向量和量化后的样本进行距离度量。上图展示了这两种方式,其中 x 和 y 分别表示查询向量和样本向量,q(x) 和 q(y) 表示使用码本量化后的向量。
对于 ADC 算法,距离的期望误差上界只与量化误差有关,与输入的 x 无关。而对于 SDC 算法,距离的期望误差上界是 ADC 的两倍,因此通常更倾向于使用 ADC 算法。
Inverted Multi-Index
2014年发表在TPAMI上的论文 The Inverted Multi-Index 提出了一种基于倒排索引的改进聚类算法Inverted Multi-Index(IMI)索引。在同等条件下,IMI 相比传统的 Inverted File(IVF)索引具有更高的性能表现和更好的召回率,并且内存空间占用更小。
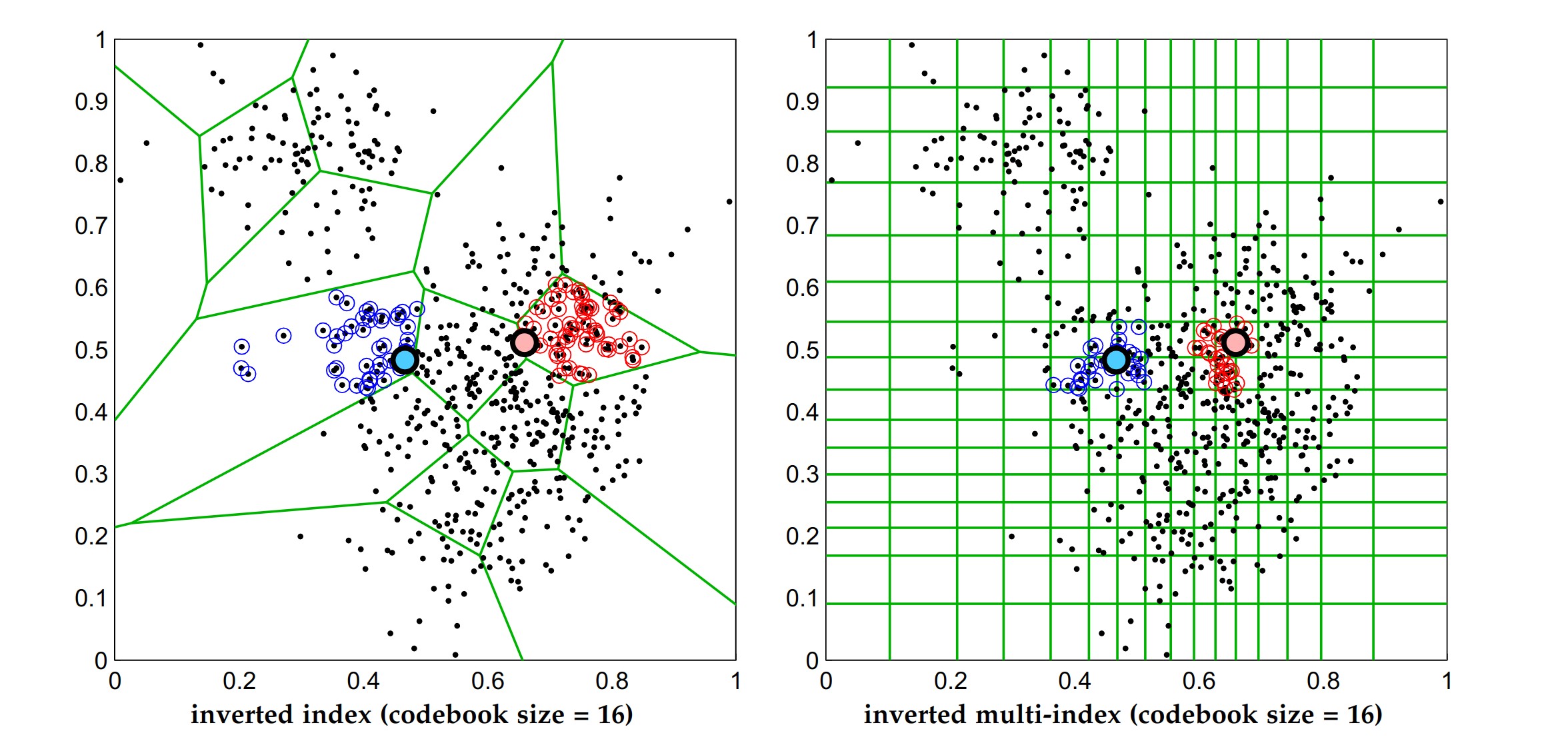
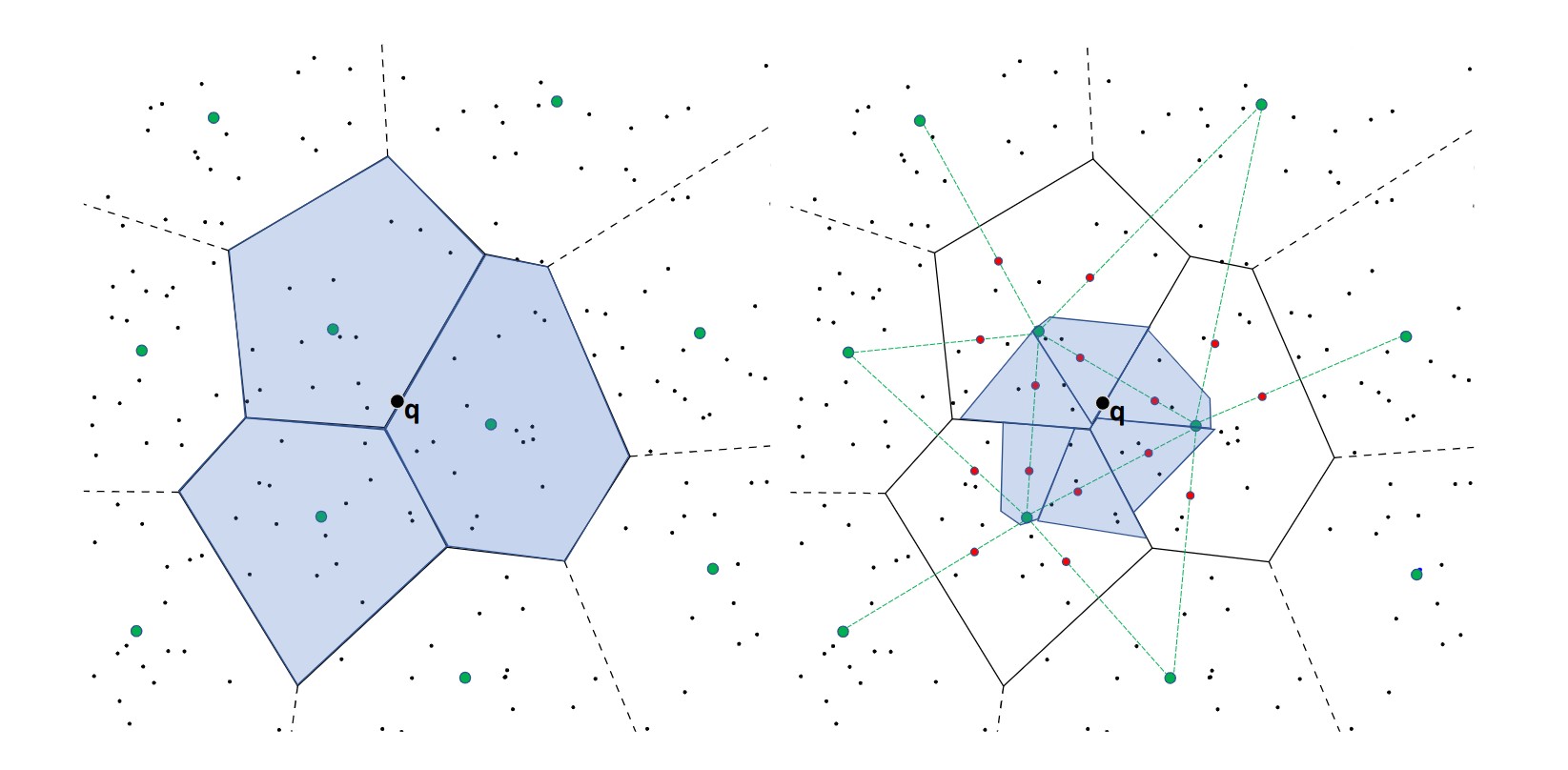
传统的倒排索引虽然可以有效地过滤大量数据点,然而在海量数据(十亿级别)的情况下,IVF 对数据空间的划分仍然不够均衡,查询会返回一个相当大的列表,并且这个列表中的数据是相当稀疏、倾斜的(也就是返回的数据仍然不够聚集),而提高码本的大小又会降低查询的性能。
如上图所示,左图是使用倒排索引进行聚类时的查询结果,其中蓝色和红色点分别代表两次查询获得的列表。可以看到 IVF 返回的数据相当分散,尤其是当查询点落在接近聚类边缘的时候,会漏掉很多近邻数据(在使用 IVF 时通常会查询多个列表来缓解这个问题),这种情况在高维数据上更为频繁)。而右图是 IMI 算法得到的查询结果,可以看到红点和蓝点更加聚集,返回的数据更能满足实际应用需求。
受到PQ算法的启发,IMI 同样将 M 维数据空间划分为 k 个子空间,并在每个子空间内通过 K-means 算法学习得到一个大小为 l 的码本 {w_1, w_2, \dots, w_l}。生成聚类中心后,需要将每个部分的聚类中心拼接以后才能完全代表数据集中的数据,因此总共存在 l^k 个列表。为避免过多的列表,通常会选择 k=2 。
对于每条原始数据,将其分为 k 个子向量,并通过之前学习得到的码本找到每个子向量对应的最近聚类中心 i,拼接这些聚类中心后,就能得到对应的列表 {i_1, i_2, \dots, i_k} 。整个向量的距离计算方式为每个子向量距离的和。
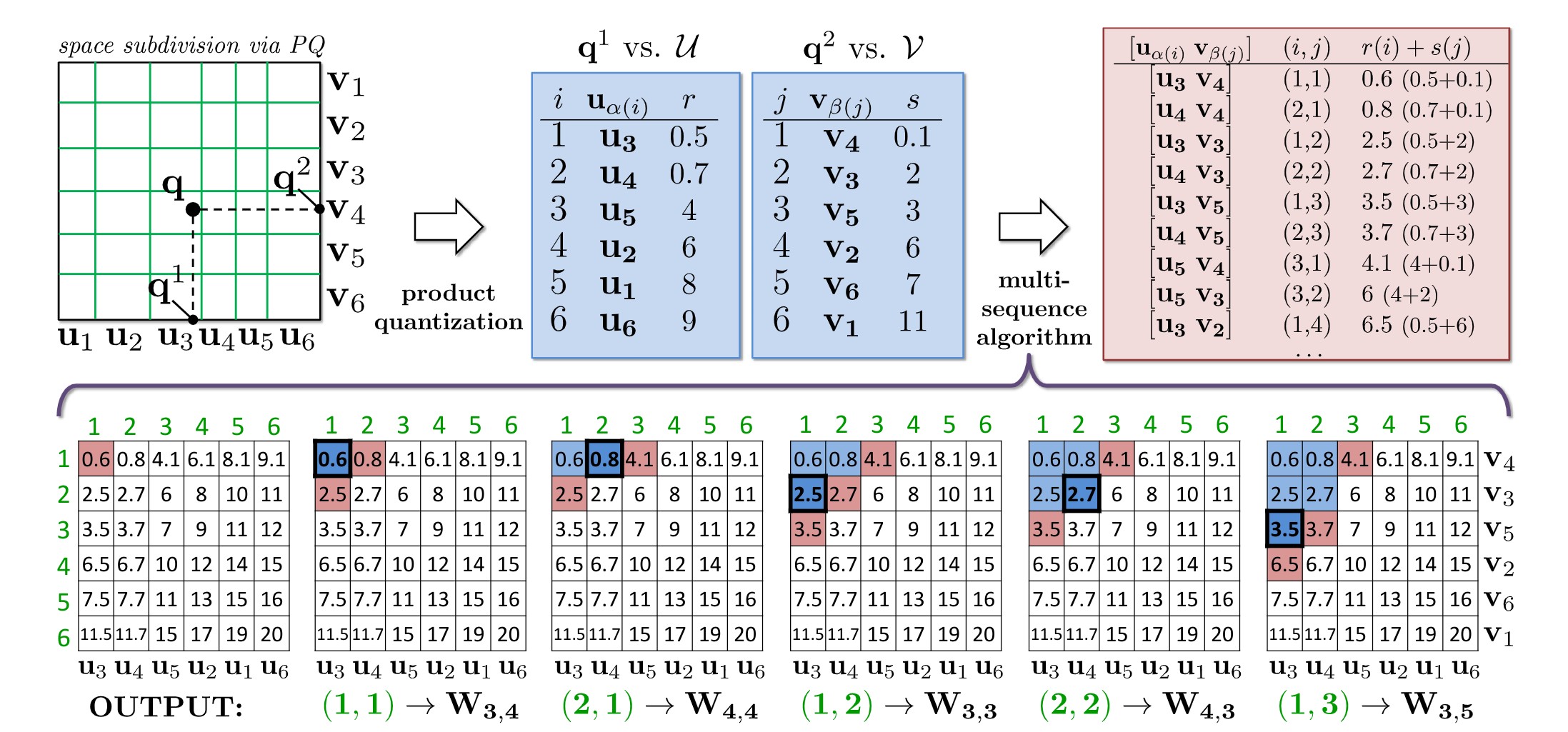
IMI 的搜索过程也很简单。如上图所示,将查询向量同样分为 k 段,对每段向量使用 ADC 算法,计算并选取其中 T 个相似度最高的中心,图中选择了 T=6。将每个子向量获得中心列表进行拼接,得到 T^l 个子列表,最后在这些子列表中找到距离查询向量最近的 top T 个结果。该过程的时间复杂度为 O(T)。更详细的搜索流程请参考原论文。
上面描述的查询流程中,距离的计算使用的是 ADC,对应的算法成为 Multi-ADC。为了提高精度,论文中还提出了一种优化:将每个向量本身和聚类中心之间的残差向量再通过 Multi-ADC 编码进行保存,称为 Multi-D-ADC。Multi-D-ADC 比 Multi-ADC 有更高的召回率,Multi-ADC 则比 Multi-D-ADC 的计算速度更快,具体使用哪种方式需要根据场景权衡。
IVF-HNSW
这篇发表于 2018 年 ECCV 会议上的论文 Revisiting the inverted indices for billion-scale approximate nearest neighbors 分析了在大规模数据上,倒排索引相对于 Inverted Multi-Index(IMI)的优势,并通过使用 HNSW 算法缓解其不足,从而实现了更优秀的近似最近邻搜索算法。
虽然 Inverted Multi-Index 在精度上更为优秀,但其存在的问题是:因为不同子空间之间可能高度相关,划分得到的很多子区域中都没有数据点,这会导致有效区域数量较少,使搜索花费大量时间在空区域中。虽然 IMI 能够获得更精确的候选列表,并且在 K 较小时查询效率高,但随着 K 的增加,IMI 存在大量随机内存访问,同时内存消耗急剧增加,而倒排索引对数据量的扩展性更好。因此,在大数据量的场合下,倒排索引具有更大的潜力。基于此,作者提出了对 IVF 的优化算法——IVF-HNSW。
IVF 使用聚类的方法将数据划分成多个区域(region),而 IVF-HNSW 在此基础上进一步将每个区域划分为多个子区域(subregion)。与第一次划分不同的是,为了避免过高的内存需求,IVF-HNSW 提出了一种不依赖于 K-means 的子区域划分算法,称为"grouping"。
grouping 对于每个区域都是独立进行的,假设某区域聚类得到的中心为 c,对应的数据为 {x_1, x_2, \dots, x_n},记 s_1, \dots, s_L \in C 为 c 最邻近的 L 个中心。
我们令区域的子中心为 {c+\alpha (s_l -c)}, l=1,\dots,L,其中 \alpha 的取值放在后面描述。对于每个 x_i,可以获得距离最近的子中心:
$$
l_i = argmin || x_i - (c + \alpha(s_l - c)) ||^2
$$
之后就可以按照 IVF-ADC 的思路,对 x_i − (c + \alpha(s_li − c)) 进行量化,使用了子中心后,偏移量相对于 IVF-ADC 会小不少,因此压缩效果也会更好。
上图中,绿色点就是聚类获得的中心,而红色点就是每个聚类计算得到的子中心,这里取 L=5。
对于任意的查询 q,其和每个子区域的中心距离 \left\Vert q - c - \alpha(s_l - c) \right\Vert ^ 2 可以通过一些预计算快速得到(怎么快速计算的就不展开了,主要是这破wp写latex太好用了)。如果总共需要访问 k 个区域,那么其中包含了 kL 个子区域,通过测试发现,即使通过距离过滤掉一半的子区域,准确率也不会下降特别严重。因此设置了一个参数 \tau,指定访问子区域的比例,如上图右中,\tau = 0.4。
剩下的问题就在于如何确定 \alpha 的取值,对于每个区域来说,我们希望通过求解如下问题来获得最优的 \alpha 参数:
也就是希望使每一个数据点和最近子中心的距离都尽可能小,这个问题的求解相对复杂,这里给出了一种近似求解方式:
首先对每个数据点 x_i 通过如下最优化问题计算最优的子中心 s_i
对于每个子问题,可以对 l_i 进行枚举:对于每个固定的 l_i 都可以计算出最优的 \alpha 值,待回原式就能得到每个 x_i 对应的 l_i。最后,将计算出的所有 s_i 值待会原式,求解得到 \alpha
那么问题来了,HNSW 在哪?由于这里考虑的是 billion 级的数据量,因此 IVF 聚类的中心数量也会相当多,为了提高码本的搜索速度,使用了 HNSW 来对所有中心构建索引,能够在几乎不降低准确率的情况下大大提高查询效率。
HNSW
DiskANN
https://suhasjs.github.io/files/diskann_neurips19.pdf
SPANN
https://arxiv.org/abs/2111.08566