内存分配算法
Linear Allocator
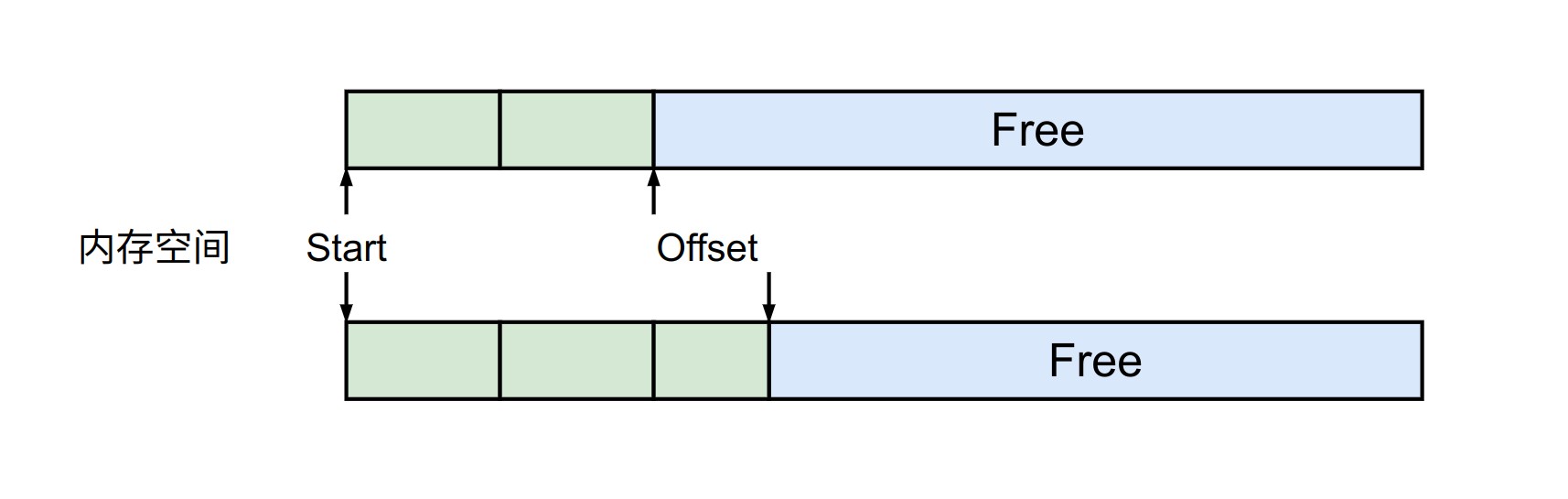
Linear Allocator 的核心思想非常简单,给定一块预分配的内存空间,该分配器会在这块内存空间上持续进行空间分配。
Linear Allocator 的接口非常简单,只有两个接口:Allocate 和 Reset 。
整个分配过程如下图所示,由于不需要进行 Deallocate,空间的分配也异常的简单。
这种分配算法有很大的限制,但在一些特定场景里却很有用,例如在某些逻辑中,需要创建大量的小对象,并且这些对象会在使用完毕后同时进行释放,此时 Linear Allocator 就能极大的提高分配效率。
Fixed Size Allocator
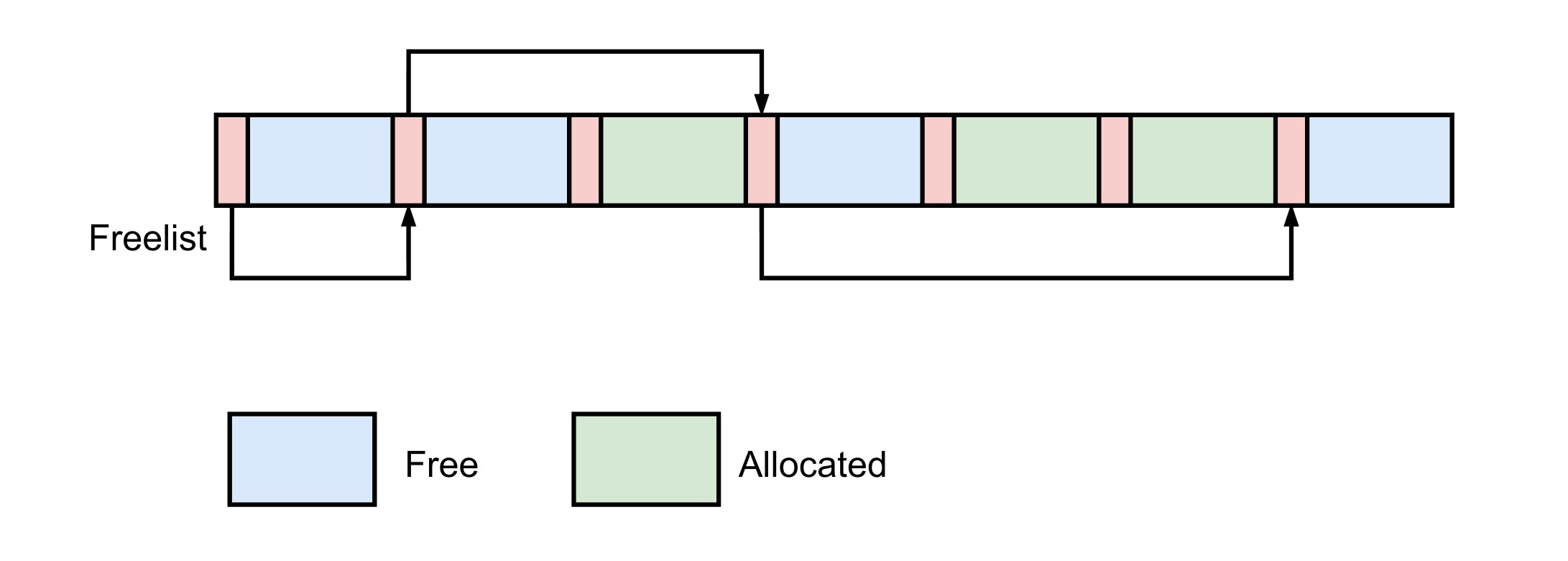
顾名思议,Fixed Size Allocator 只能分配和释放固定大小的内存。它的核心思想是预创建内存块,然后将内存块切割成多个固定大小的小块,并将它们链接起来形成一个freelist
- 分配的时候从 freelist 取出小块返回
- 释放的时候将小块重新链接回 freelist
整个分配过程如下图所示,此算法的理解和实现同样也很简单。虽然只能分配固定大小的内存,但它是很多现代内存管理器的重要组成部分,例如 slab allocator。
Freelist Allocator
Freelist Allocator 可以看作是 Fixed Size Allocator 的泛化版本,它不会将内存空间切分为多个固定大小的块,而是在分配时动态切分。
初始状态时,Allocator 内只有一块内存,我们会使用一个链表来存储内存中空闲块的地址以及其大小。
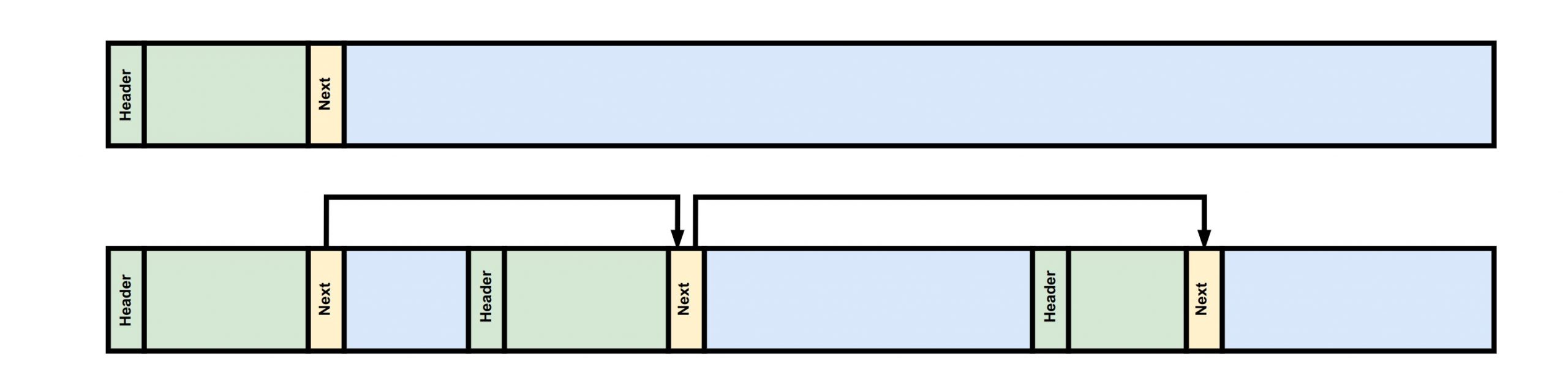
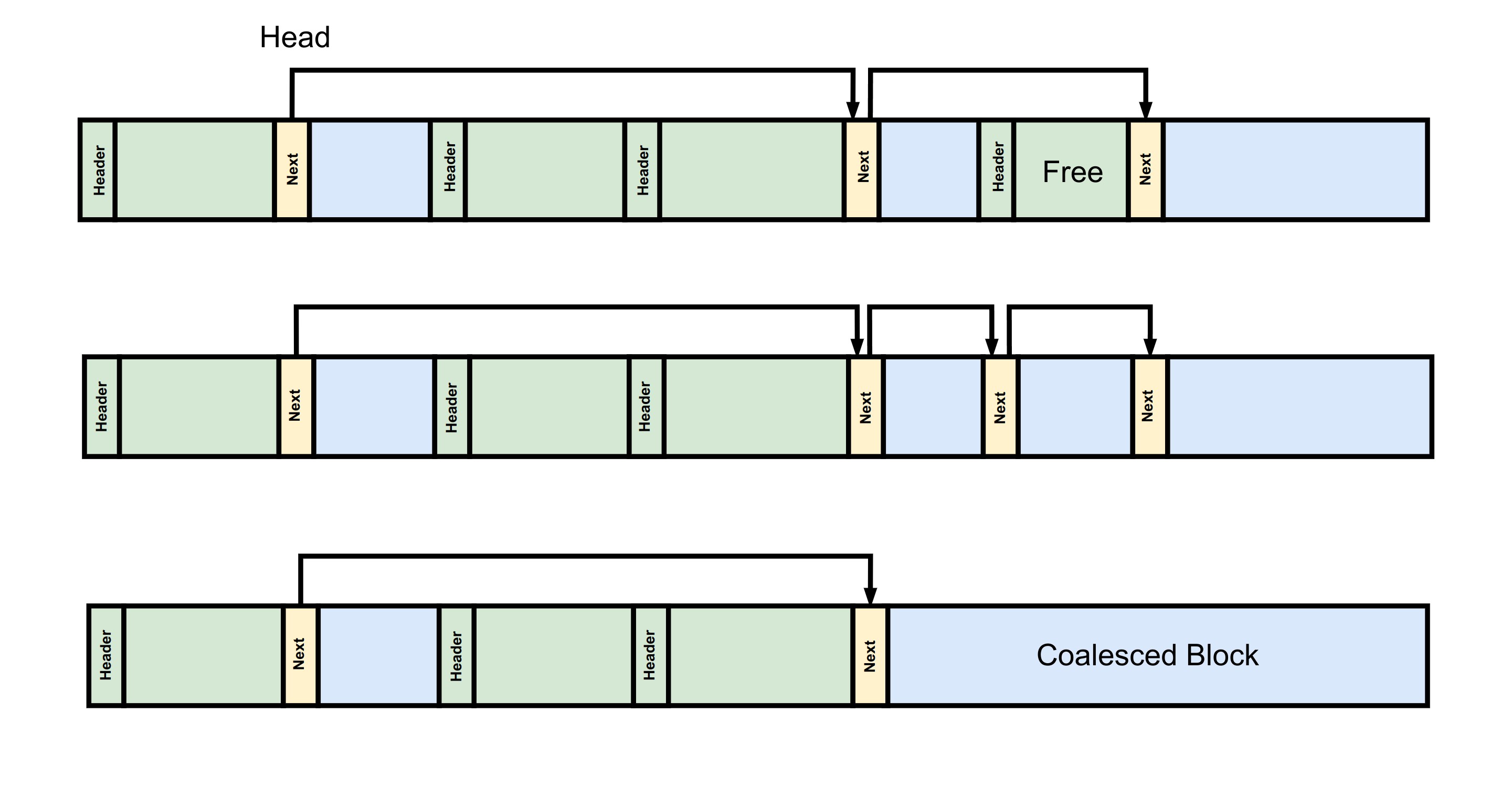
当用户请求内存时,系统会在链表中查找一个能够容纳用户请求大小的空闲块,将其从链表中删除并返回给用户。由于内存分配时没有使用固定的块大小,因此在返回的空间之前需要设置一个 header 来记录该块的大小,以便在释放内存时进行操作。下图就描述了在若干次分配和释放之后的内存空间状态。
在下图中,当出现新的内存请求时,系统遍历空闲链表并发现第二块和第三块都可以容纳该请求的大小。因此,系统选择从第二块中分配所需的空间,并更新空闲链表以反映该块的变化。当分配器内存在多个合适的空闲块时,会根据相应的策略选择其中一块进行分配,策略通常有两种:
- First fit: 查找第一个可用块
- Best fit: 查找一个可容纳请求大小的最小空闲块。该策略可以减少分配器内存碎片。
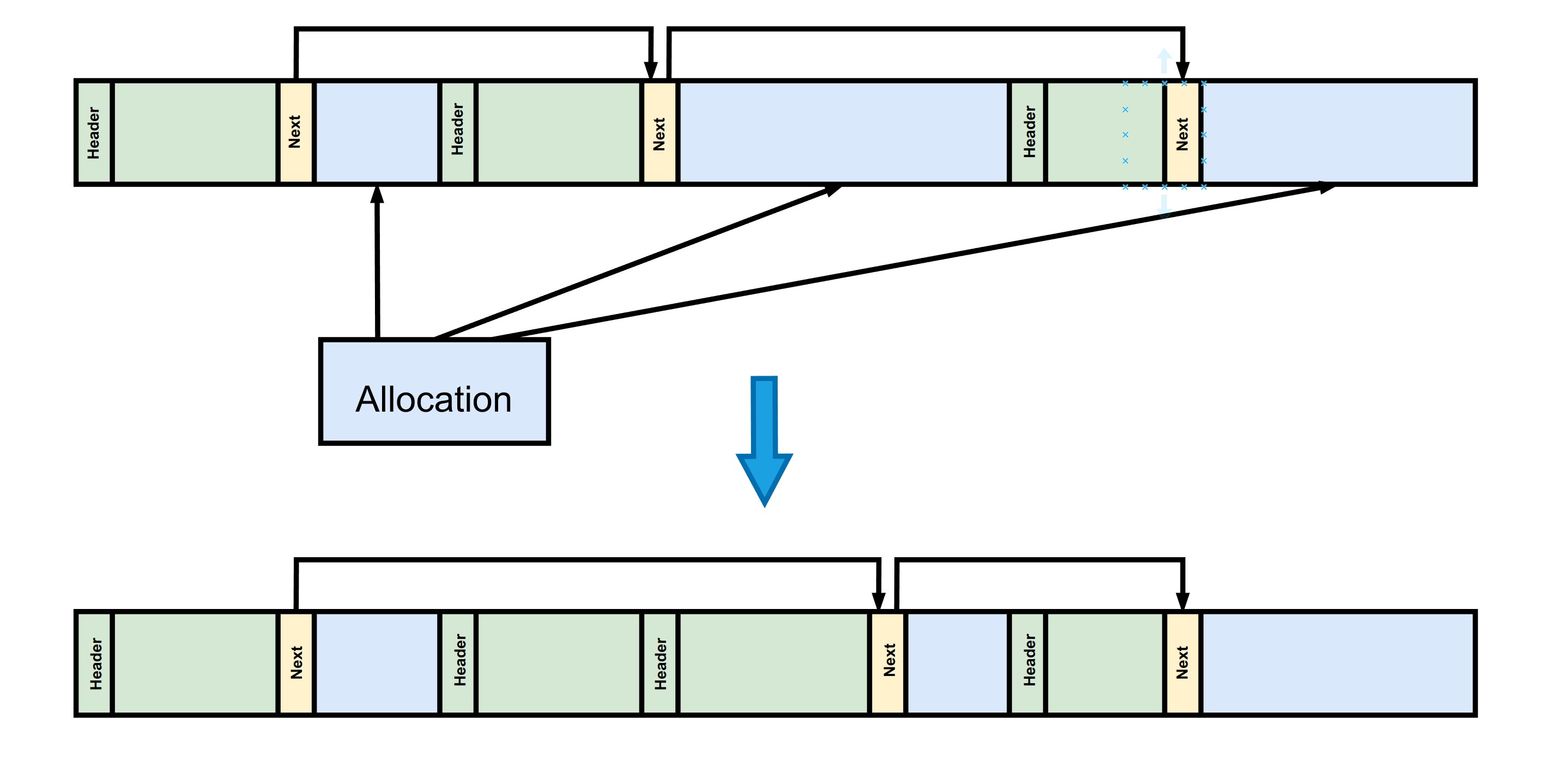
下图展示了在该分配器内部进行释放的过程。在释放一个空闲块后,需要将其加入到空闲链表中,这里我们会维持空闲链表的有序性,因此会遍历链表找到合适的插入位,其时间复杂度为O(N),其中N为空闲列表的长度。除此之外,我们还会将相邻的空闲内存块进行合并,得到更大的空闲块,避免后续的分配由于过多的内存碎片失败。
Buddy Allocator
基本思想
终于到了 Buddy Allocator,这部分才是这篇文章的核心(醋找到了),我们先来看看 ChatGPT 怎么介绍的:
Buddy allocator 是一种内存分配算法,它可以在动态内存分配时高效地管理内存块。Buddy allocator 的基本思想是将可用内存块划分为大小相等的块,每个块的大小都是 2 的幂次方,例如 2^0, 2^1, 2^2, 2^3 等等。每个大小相等的内存块都被称为“伙伴块”。
当一个内存分配请求到达时,buddy allocator 会查找大小最接近请求大小的可用块。如果找到的块比请求的块大,就将它一分为二,形成两个大小相等的伙伴块。其中一个伙伴块被分配给请求者,另一个伙伴块被标记为可用。如果找到的块大小恰好等于请求的块大小,那么它就被直接分配给请求者。
当一个内存释放请求到达时,buddy allocator 会检查被释放的块的伙伴块是否也被释放了。如果伙伴块也被释放了,那么这两个伙伴块会被合并成一个更大的块,然后继续检查它们的伙伴块是否被释放。这个过程会一直进行下去,直到找到一个未被释放的伙伴块或者到达了内存池的顶部。
Buddy allocator 的优点是可以高效地管理内存块,降低内存碎片的产生率,而且它的内存分配和释放操作都是比较快速的。缺点是它需要维护一个内存块的伙伴关系,而且如果内存池中的内存块大小不够灵活,可能会浪费一部分内存空间。
不得不说,ChatGPT 真的很强,上面的介绍已经把算法的核心思想都给说明了,不过在没有接触过该算法的时候,可能没办法完全理解,比如什么是伙伴?(正义的伙伴.jpg)
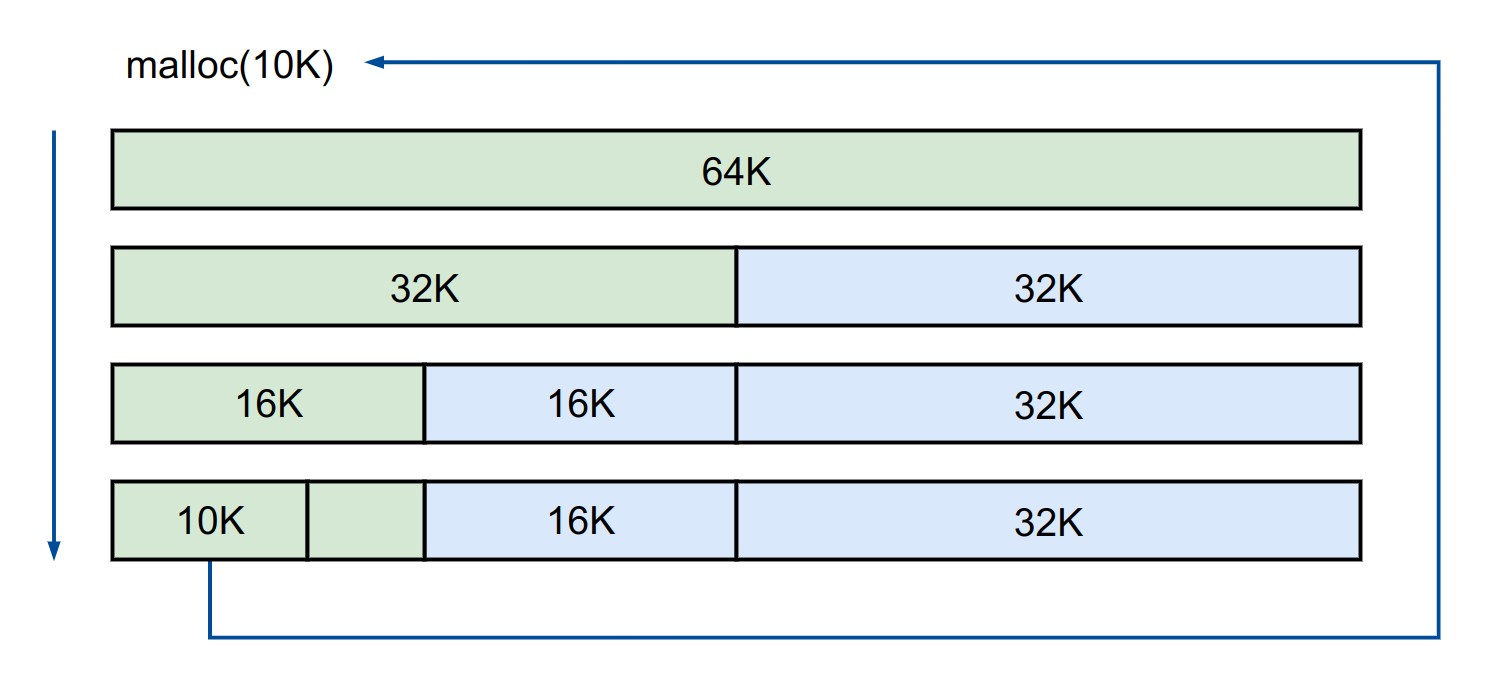
Buddy 的分配其实是一种二分的思想,举个栗子,例如我们要从64K的空间里划分出一块10K的空间时,分配过程如下:
- 初始状态时我们拥有一块64K的空间,对其一分为二,获得两块32K的空间,其中一块用于继续划分,另一块标记为空闲
- 将第一块32K的空间继续划分为两个16K的空间,同样的,第一块用于继续划分,另一块标记为空闲
- 由于16K不能再进行划分,否则空间会小于10K,因此将第一块16K的空间标记为已分配,并返回其地址
分配完成之后,图中蓝色块即空闲块,而绿色块即已分配的空间。
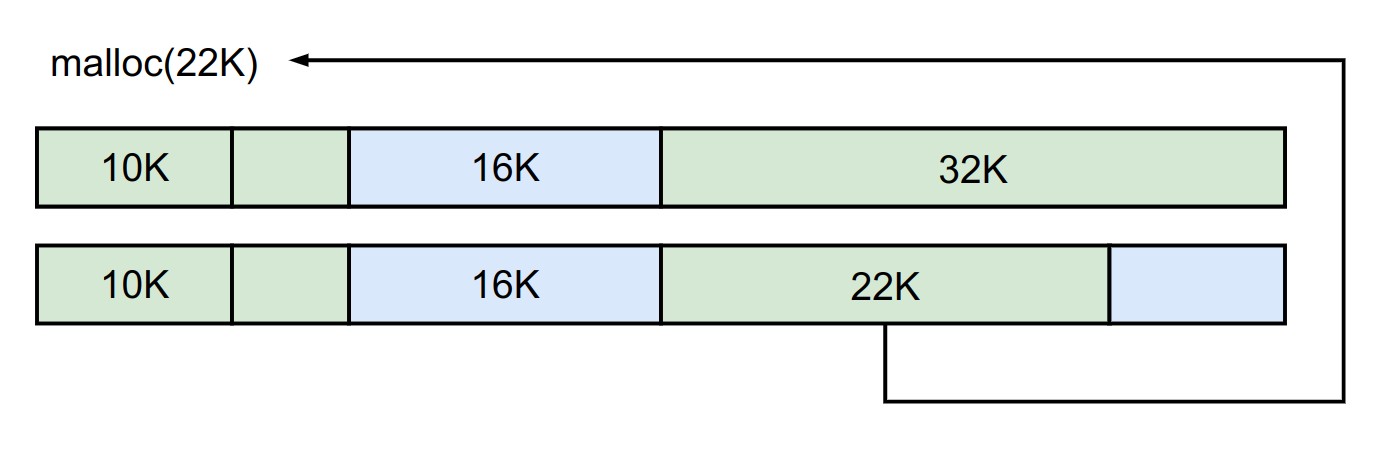
如果我们要再分配一块 22K 的空间,此时我们能找到的空闲块是在第一步中切分出来的32K空间,由于其不能继续切分,所以直接返回,最终空间分配如下图所示,
上述的描述和 ChatGPT 给出的第二段其实是对应的,如果不考虑释放的话,Buddy Allocator 的原理也就是这些内容,听上去似乎比较简单,接下来就是怎么从代码层面去实现这个分配器了。这里我们会以 6.S081 的 Lab3 例进行介绍。
代码实现
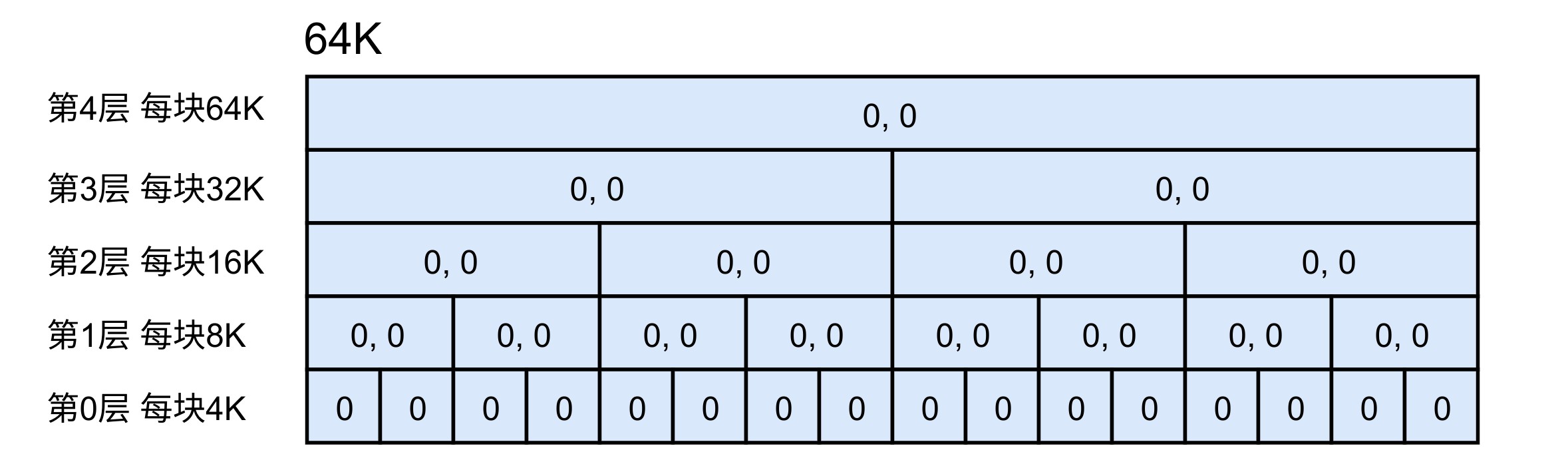
在 Buddy Allocator 中需要设置最小的划分是多大,代码中用 LEAF_SIZE 表示。这里假设总空间大小为64K,LEAF_SIZE 为 4k,如图所示,共有1块64K的空间,2块32K的空间,以此类推。为了便于描述,将第 i 层的第 j 块记为 b(i,j),初始状态如下:
什么是伙伴?伙伴就是相邻的两个块,例如 b(2,0) 和 b(2,1)、b(3,2) 和 b(2,3),第0层有8组伙伴,第一层有4组伙伴,以此类推。为了便于表述,将一组伙伴称为伙伴对,每个块上一层的块称为其父块,例如 b(1,1) 的父块是 b(2,0)
对于每个块来说,需要记录两个属性:split, alloc,split 表示该块已经被切分了,alloc 表示该块已经被分配。这两个属性在内存释放中会起到作用。
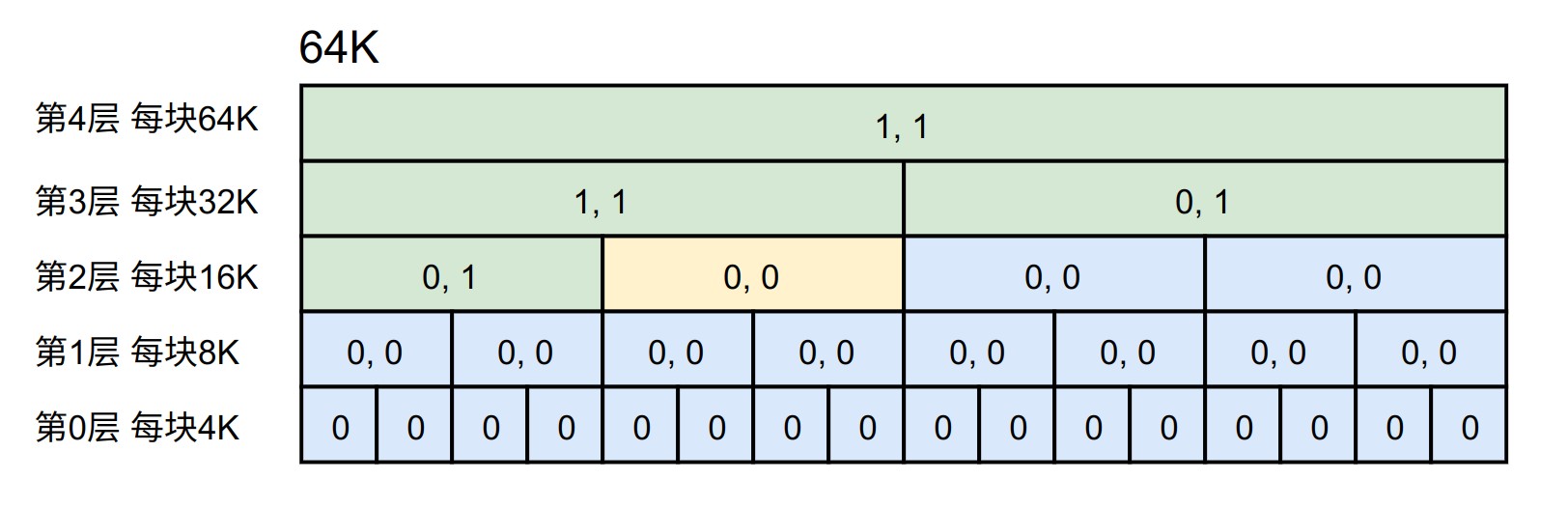
在上一节中的栗子中,分配 10K 和 22K 之后,整体空间就会如下所示,其中黄色块为空闲块,这里只有 b(2,1) 空闲,b(2,0) 和 b(3,1) 被进行了分配,状态为 {0, 1}。
buddy.c 中为每一层定义了一个如下的 sz_info 结构体,它包含3个字段:free、alloc 以及 split,其中 free 存储每一层的空闲块地址,split 数组记录了内存块是否被切分,alloc 数组记录了该层的内存块是否已被分配。注意这些元信息也是存储在给定的内存空间中的。
struct sz_info {
Bd_list free;
char *split;
char *alloc;
};
typedef struct sz_info Sz_info;
static Sz_info *bd_sizes; 初始化
分配器的初始化流程如下:
- 首先会初始化所有元信息,所有空闲链表为空。
- 由于元信息也存储在内存空间里,之后需要把对应的内存区域标记为不可分配(这里我们先不考虑内存对齐问题,否则还需要额外标记一些不可分配的空间)。
- 最后找到更新之后的所有空闲块加入对应链表。
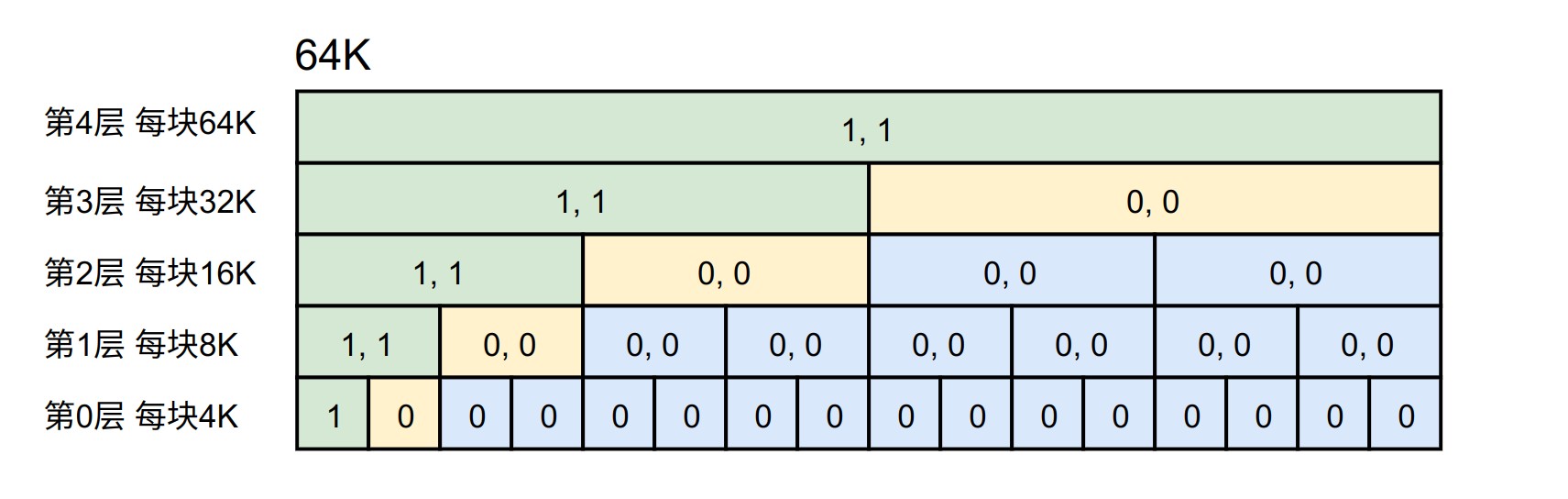
步骤2中标记不可分配的动作其实就是将所有和对应区域有重叠的块标记为已分配,只需要遍历每一层,找出和目标区间有重叠的块即可,如下图所示,假设元信息需要 4K 的空间(向上对齐到4K),对应区域就是 [0, 4K),绿色块就是被标记为不可分配的块。
步骤3从肉眼看感觉也是很简单的步骤,黄色块就对应了所有空闲块,实际的实现是比较 tricky 的,这里先不描述了,知道结果就可以了。(啥时候想到了再补吧)
分配
分配大小为 m 的空间的流程和前述的示例几乎是一样的,稍加翻译就能得到如下步骤:
- 计算 m 应该被放置在的层数 l
- 从第 l 层向上查找空闲链表,找到第一个空闲块 b(i,j),b(i,j) 一定是满足大小要求的最小空闲块。如果没有找到空闲块,直接返回空。
- 如果不需要切分,将 b(i,j) 的属性设为
0, 1,表示未切分、已分配,移出空闲链表并返回其地址 - 否则,将 b(i,j) 的属性标为
1, 1,将该块移出空闲链表,将其第二个子块加入对应的空闲链表,对第一个子块跳转步骤3迭代处理。
来看一下对应的代码
void *bd_malloc(uint64 nbytes) {
int fk, k;
// Find a free block >= nbytes, starting with smallest k possible
fk = firstk(nbytes);
for (k = fk; k < nsizes; k++) {
if(!lst_empty(&bd_sizes[k].free))
break;
}
if (k >= nsizes) { // No free blocks?
return 0;
}
// Found a block; pop it and potentially split it.
char *p = lst_pop(&bd_sizes[k].free);
bit_set(bd_sizes[k].alloc, blk_index(k, p));
for(; k > fk; k--) {
// split a block at size k and mark one half allocated at size k-1
// and put the buddy on the free list at size k-1
char *q = p + BLK_SIZE(k-1); // p's buddy
bit_set(bd_sizes[k].split, blk_index(k, p));
bit_set(bd_sizes[k-1].alloc, blk_index(k-1, p));
lst_push(&bd_sizes[k-1].free, q);
}
return p;
}首先通过 firstk 找到步骤1需要的 fk,之后不断向上遍历直到 k 层的空闲链表不为空,取出空闲块后,再不断向下分裂到 fk 层。每次循环中,p 指向待分裂的块,q 则是分裂后对应的 buddy,需要加入空闲链表。
释放
释放地址为 p 的空间相对会复杂一些,首先需要确定的就是待释放的指针对应的空间大小。通过观察可以发现:第 l 层的块如果被分配了,那么其所有子块的 split 值都为0(因为其子块不可能被分配),同时其父块的 split 值为1(父块切分后才能得到当前块)。因此整个释放流程如下,其对应了 ChatGPT 介绍中的第三段:
- 从下向上遍历每一层 l,找到 p 所在的块 b_l,如果 b_l 的
split为1,退出循环。p 所在的层为 l-1,对应的块记为 b - 找到 b 的 buddy,如果 buddy 已被分配,将 b 的属性修改为
0, 0并加入该层的空闲队列,返回 - 否则需要将伙伴对合并,将 b 和 buddy 的属性同时修改为
0, 0并加入该层的空闲队列,令 b 为其父块,回到步骤2
看看代码
// Free memory pointed to by p, which was earlier allocated using
// bd_malloc.
void bd_free(void *p) {
void *q;
int k;
for (k = size(p); k < MAXSIZE; k++) {
int bi = blk_index(k, p);
int buddy = (bi % 2 == 0) ? bi+1 : bi-1;
bit_clear(bd_sizes[k].alloc, bi); // free p at size k
if (bit_isset(bd_sizes[k].alloc, buddy)) { // is buddy allocated?
break; // break out of loop
}
// budy is free; merge with buddy
q = addr(k, buddy);
lst_remove(q); // remove buddy from free list
if (buddy % 2 == 0) {
p = q;
}
// at size k+1, mark that the merged buddy pair isn't split anymore
bit_clear(bd_sizes[k+1].split, blk_index(k+1, p));
}
lst_push(&bd_sizes[k].free, p)
}size 函数完成的工作就是找到步骤1所指的 l-1,if (buddy % 2 == 0) 这里的判断就是确定父块地址的过程,因为伙伴对左侧的地址和其父块的地址是相同的。
后记
到这里为止,所描述的代码都是 6.S081 给出官方的实现。这一部分的任务为优化 Buddy Allocator 中的 alloc 数组,这里就不再赘述了,问题并不算难实现,这个链接 讲的还是不错的。
(也许是因为我直接看的别人的解析所以觉得简单;另外网上找到的实现基本都点小虫子,得自己捉一捉。)



优秀!!